Pendahuluan
Selamat datang di Rintiksedu.id! Saya sangat senang bisa berbagi pengalaman dan pengetahuan seputar cara memfaktorkan pertidaksamaan kuadrat dengan Anda. Dalam artikel ini, saya akan menjelaskan berbagai metode, tips, dan trik yang dapat Anda gunakan untuk memfaktorkan pertidaksamaan kuadrat dengan mudah dan efisien. Gambar unggulan kami akan membantu Anda memvisualisasikan langkah-langkah yang diperlukan dalam proses tersebut.
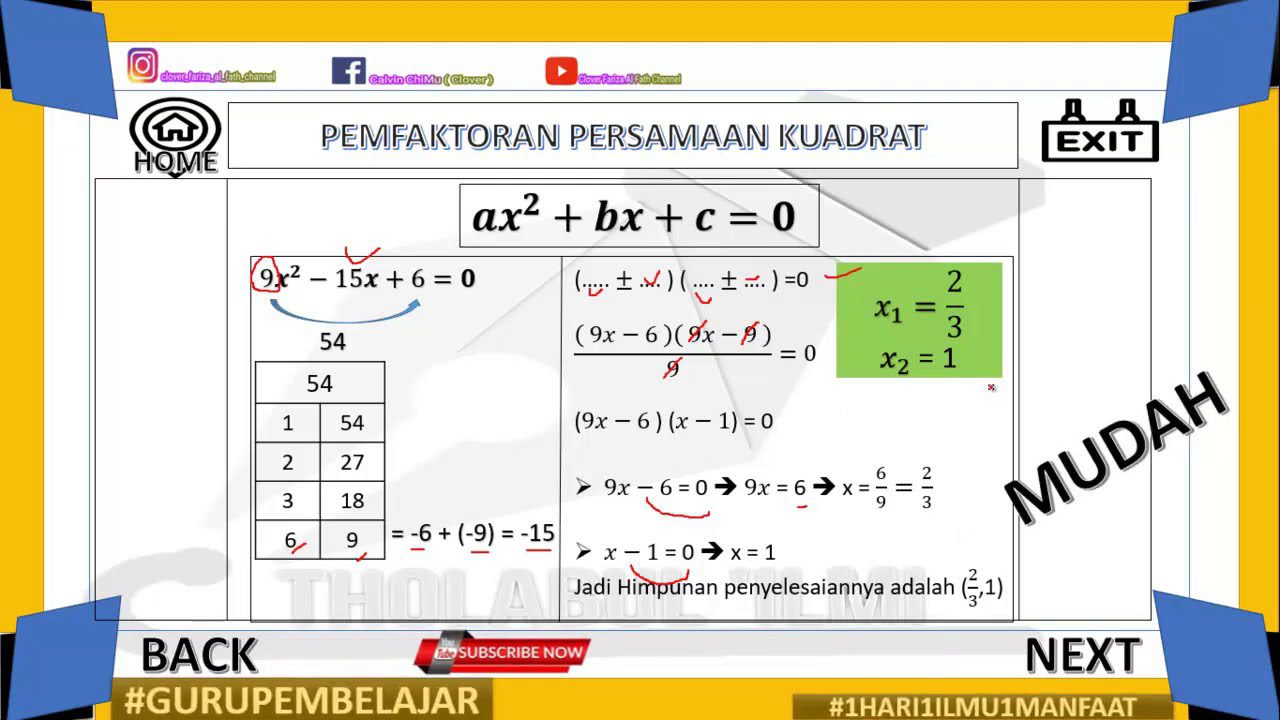
Mengapa Memfaktorkan Pertidaksamaan Kuadrat Penting?
Memahami cara memfaktorkan pertidaksamaan kuadrat adalah keterampilan yang sangat penting dalam matematika. Pertidaksamaan kuadrat adalah bentuk persamaan matematika yang melibatkan kuadrat dari satu atau lebih variabel. Dalam kehidupan sehari-hari, kita sering perlu memecahkan pertidaksamaan kuadrat untuk mencari akar-akar persamaan atau menyelesaikan masalah yang melibatkan model matematika. Dengan menguasai teknik-teknik faktorisasi yang tepat, Anda akan lebih efektif dalam memecahkan masalah matematika yang melibatkan pertidaksamaan kuadrat.
Metode Faktorisasi Pertidaksamaan Kuadrat
Ada beberapa metode yang dapat Anda gunakan untuk memfaktorkan pertidaksamaan kuadrat. Berikut adalah tiga metode yang paling umum digunakan:
1. Faktorisasi melalui Penyebaran dan Penggabungan
Metode pertama yang akan kita bahas adalah faktorisasi melalui penyebaran dan penggabungan. Cara ini melibatkan penyebaran (distribusi) faktor-faktor bersama terbesar dari suku-suku pertidaksamaan kuadrat dan kemudian penggabungan faktor-faktor yang sama.
Contoh:
Kita ingin memfaktorkan pertidaksamaan kuadrat x^2 – 5x + 6.
Kita memulai dengan mencari dua bilangan yang ketika dijumlahkan menghasilkan -5 dan ketika dikalikan menghasilkan 6. Dalam kasus ini, bilangan tersebut adalah -2 dan -3.
Jadi, pertidaksamaan kuadrat dapat difaktorkan menjadi (x – 2)(x – 3).
2. Faktorisasi melalui Menggunakan Rumus kuadrat
Metode kedua yang dapat Anda gunakan untuk memfaktorkan pertidaksamaan kuadrat adalah dengan menggunakan rumus kuadrat yaitu x = (-b +- akar(b^2 – 4ac)) / 2a.
Contoh:
Kita ingin memfaktorkan pertidaksamaan kuadrat x^2 – 5x + 6.
Dalam kasus ini, a = 1, b = -5, dan c = 6.
Jadi, kita dapat menggunakan rumus kuadrat untuk menentukan dua akar pertidaksamaan kuadrat, yaitu x = 2 dan x = 3.
Maka, pertidaksamaan kuadrat dapat difaktorkan menjadi (x – 2)(x – 3).
3. Faktorisasi melalui Penyelesaian Persamaan Linier
Metode ketiga yang akan kita bahas adalah faktorisasi melalui penyelesaian persamaan linier. Cara ini melibatkan penyelesaian persamaan linier terlebih dahulu dan kemudian memfaktorkan persamaan tersebut.
Contoh:
Kita ingin memfaktorkan pertidaksamaan kuadrat x^2 – 5x + 6.
Kita dapat menyelesaikan persamaan linier x^2 – 5x + 6 = 0 dengan menggunakan metode faktorisasi, rumus kuadrat, atau metode penyelesaian lainnya. Dalam kasus ini, kita dapat mencari dua akar persamaan linier: x = 2 dan x = 3.
Maka, pertidaksamaan kuadrat dapat difaktorkan menjadi (x – 2)(x – 3).
Tabel Perbandingan Metode Faktorisasi
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Penyebaran dan Penggabungan | Mudah dipahami dan diaplikasikan | Tidak efisien untuk pertidaksamaan dengan variabel yang sangat besar |
| Rumus Kuadrat | Menghasilkan akar-akar persamaan secara cepat | Sulit diterapkan jika koefisien persamaan tidak sederhana |
| Penyelesaian Persamaan Linier | Metode yang fleksibel, dapat digunakan dalam berbagai kasus | Dapat memerlukan langkah-langkah tambahan dalam beberapa kasus |
FAQ
1. Apa itu pertidaksamaan kuadrat?
Jawaban: Pertidaksamaan kuadrat adalah bentuk persamaan matematika yang melibatkan kuadrat dari satu atau lebih variabel, biasanya ditulis dalam bentuk ax^2 + bx + c > 0 atau ax^2 + bx + c < 0, di mana a, b, dan c adalah konstanta dan x adalah variabel yang tidak diketahui.
2. Mengapa penting untuk memfaktorkan pertidaksamaan kuadrat?
Jawaban: Memfaktorkan pertidaksamaan kuadrat memungkinkan kita untuk menemukan akar-akar persamaan, memahami pola-pola dalam grafiknya, dan memecahkan masalah matematika yang melibatkan pertidaksamaan kuadrat secara lebih efisien.
3. Berapa banyak akar yang dimiliki oleh pertidaksamaan kuadrat?
Jawaban: Pertidaksamaan kuadrat memiliki maksimal dua akar, yaitu akar riil atau imaginer. Namun, dalam kebanyakan kasus, pertidaksamaan kuadrat memiliki dua akar riil atau tidak memiliki akar riil sama sekali.
4. Bagaimana cara menentukan tanda pertidaksamaan kuadrat?
Jawaban: Untuk menentukan tanda pertidaksamaan kuadrat, Anda dapat mencari titik-titik kritisnya, yaitu titik-titik di mana pertidaksamaan kuadrat sama dengan nol. Jika Anda tidak dapat menemukan titik-titik kritis, Anda juga dapat menggunakan metode lain seperti mencoba nilai-nilai di setiap interval pada grafik pertidaksamaan kuadrat.
5. Apa perbedaan antara faktorisasi pertidaksamaan kuadrat dan penyelesaian persamaan kuadrat?
Jawaban: Faktorisasi pertidaksamaan kuadrat melibatkan mencari faktor-faktor yang dapat menghasilkan persamaan kuadrat, sedangkan penyelesaian persamaan kuadrat melibatkan mencari akar-akar persamaan kuadrat secara langsung dengan menggunakan rumus kuadrat atau metode lainnya.
6. Apakah metode faktorisasi pertidaksamaan kuadrat selalu berhasil?
Jawaban: Tidak, metode faktorisasi pertidaksamaan kuadrat tidak selalu berhasil. Ada kasus-kasus tertentu di mana pertidaksamaan kuadrat tidak dapat difaktorkan dengan mudah menggunakan metode faktorisasi konvensional. Dalam kasus tersebut, Anda dapat menggunakan rumus kuadrat atau metode lainnya untuk menyelesaikan pertidaksamaan kuadrat.
7. Apa yang harus dilakukan jika pertidaksamaan kuadrat tidak dapat difaktorkan atau diselesaikan?
Jawaban: Jika pertidaksamaan kuadrat tidak dapat difaktorkan atau diselesaikan menggunakan metode konvensional, Anda dapat menggunakan metode numerik atau algoritma khusus untuk mendekati akar-akar persamaan tersebut.
8. Bagaimana cara memeriksa jawaban dari hasil faktorisasi pertidaksamaan kuadrat?
Jawaban: Anda dapat memeriksa jawaban dari hasil faktorisasi pertidaksamaan kuadrat dengan mengalikan kembali faktor-faktornya dan memastikan kembali bahwa hasil perkalian tersebut sama dengan pertidaksamaan awal.
9. Bagaimana faktorisasi pertidaksamaan kuadrat dapat diaplikasikan dalam kehidupan sehari-hari?
Jawaban: Faktorisasi pertidaksamaan kuadrat dapat diaplikasikan dalam berbagai aspek kehidupan sehari-hari, seperti dalam ilmu ekonomi untuk menganalisis hubungan antara biaya produksi dan keuntungan, dalam ilmu fisika untuk memodelkan pergerakan benda, atau dalam ilmu komputer untuk mengoptimalkan algoritma dan program.
10. Apakah ada persamaan kuadrat yang tidak dapat difaktorkan?
Jawaban: Tidak ada persamaan kuadrat yang tidak dapat difaktorkan, tetapi ada beberapa kasus di mana faktorisasi persamaan kuadrat menjadi sangat rumit atau tidak efisien dengan metode konvensional. Dalam kasus ini, Anda dapat menggunakan metode lain seperti penyelesaian persamaan kuadrat dengan rumus kuadrat atau metode numerik.
Kesimpulan
Dalam artikel ini, kita telah membahas berbagai metode, tips, dan trik untuk memfaktorkan pertidaksamaan kuadrat. Memfaktorkan pertidaksamaan kuadrat penting untuk memahami pola dan hubungan matematika, menyelesaikan masalah matematika yang melibatkan pertidaksamaan kuadrat, dan mengoptimalkan algoritma dan program. Dengan menggunakan teknik-teknik faktorisasi yang sesuai, Anda akan lebih efisien dalam memecahkan masalah matematika yang melibatkan pertidaksamaan kuadrat. Jadi, teruslah berlatih dan eksplorasi lebih lanjut tentang cara memfaktorkan pertidaksamaan kuadrat, dan semoga Anda sukses dalam perjalanan matematika Anda!







