Pendahuluan
Halo pembaca, selamat datang di Rintiksedu.id! Saya adalah penulis yang berpengalaman dalam topik seputar cara mencari suku ke n pada barisan aritmatika. Dalam artikel ini, kami akan membahas secara lengkap dan mendalam tentang rumus-rumus untuk mencari suku ke-n pada barisan aritmatika, serta memberikan contoh soal untuk memperjelas konsepnya. Gambar unggulan artikel ini bisa dilihat melalui tautan berikut
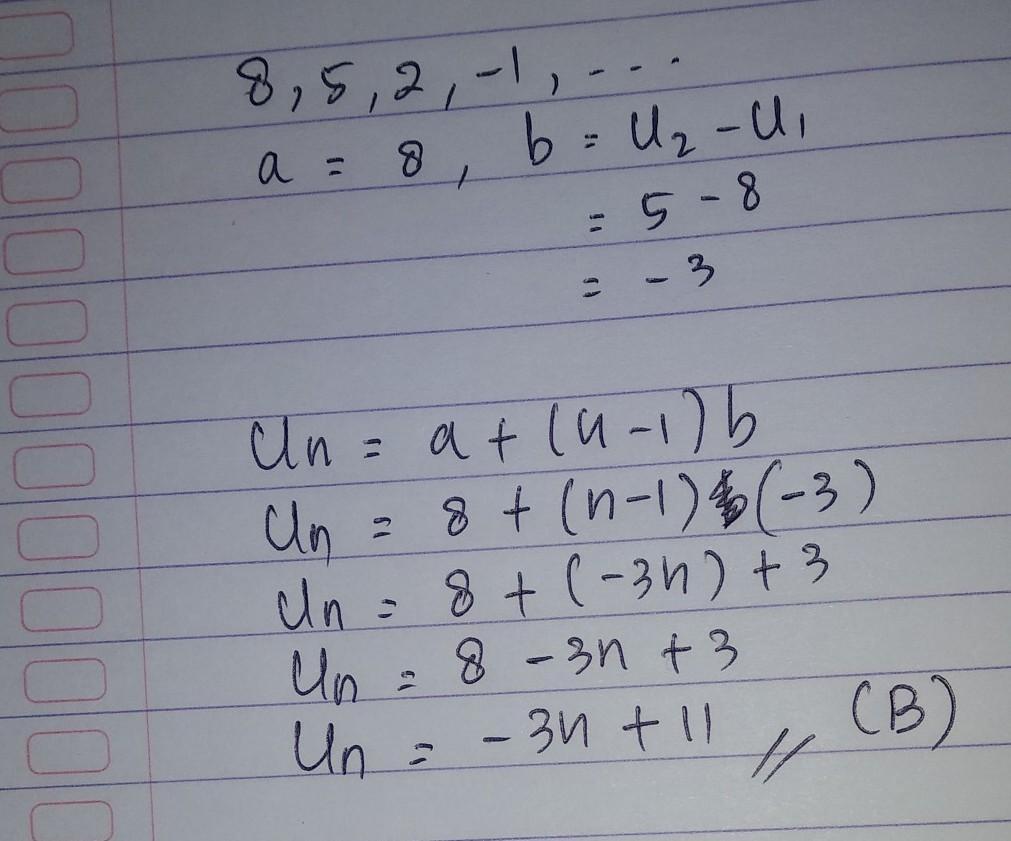
.
Pengertian Barisan Aritmatika
Apa itu Barisan Aritmatika?
Barisan aritmatika adalah rangkaian bilangan yang setiap 2 suku berturut-turut memiliki selisih yang tetap. Misalnya, 1, 4, 7, 10, … adalah barisan aritmatika dengan selisih 3. Dalam barisan aritmatika, kita dapat menggunakan rumus yang tepat untuk mencari suku ke-n. Mari kita bahas rumus-rumus yang berguna dalam mencari suku ke-n pada barisan aritmatika.
Rumus Suku ke-n Barisan Aritmatika
Rumus umum untuk mencari suku ke-n pada barisan aritmatika adalah:
Un = a + (n-1) * d
Dimana:
- Un adalah suku ke-n yang ingin dicari
- a adalah suku pertama dalam barisan
- n adalah posisi suku yang ingin dicari
- d adalah selisih antara dua suku berturut-turut dalam barisan
Pada rumus ini, kita menggunakan posisi suku ke-n dan suku pertama dalam barisan untuk menghitung suku ke-n tersebut.
Cara Menghitung Suku ke-n Barisan Aritmatika
Langkah-langkah untuk menghitung suku ke-n pada barisan aritmatika adalah sebagai berikut:
- Identifikasi suku pertama (a) dan selisihnya (d).
- Gunakan rumus Un = a + (n-1) * d untuk menghitung suku ke-n.
Sebagai contoh, misalkan kita memiliki barisan aritmatika dengan suku pertama 3 dan selisih 4. Kita ingin mencari suku ke-8 dalam barisan ini. Dalam hal ini, nilai a adalah 3, n adalah 8, dan d adalah 4. Dengan menggunakan rumus Un = a + (n-1) * d, kita dapat menghitung suku ke-8 sebagai berikut:
U8 = 3 + (8-1) * 4
U8 = 3 + 7 * 4
U8 = 3 + 28
U8 = 31
Jadi, suku ke-8 dalam barisan ini adalah 31.
Contoh Soal Rumus Suku ke-n Barisan Aritmatika
Berikut adalah beberapa contoh soal yang menggambarkan penerapan rumus suku ke-n pada barisan aritmatika:
Contoh Soal 1
Hitung suku pertama dari barisan aritmatika jika suku ketiga adalah 18 dan suku ketujuh adalah 38.
Untuk mencari suku pertama, kita dapat menggunakan rumus Un = a + (n-1) * d.
Sebagai langkah pertama, kita perlu mencari selisih (d) antara suku berturut-turut.
Untuk suku ketiga dan ketujuh, kita memiliki:
U3 = 18
U7 = 38
Untuk mencari selisih (d), kita dapat menggunakan rumus:
d = (U7 – U3) / (7 – 3)
d = (38 – 18) / (7 – 3)
d = 20 / 4
d = 5
Selanjutnya, kita dapat menggunakan rumus Un = a + (n-1) * d untuk mencari suku pertama (a).
Jika kita gunakan suku ketujuh sebagai contoh, kita dapat tulis:
U7 = a + (7-1) * 5
38 = a + 6 * 5
38 = a + 30
a = 38 – 30
a = 8
Jadi, suku pertama dalam barisan aritmatika ini adalah 8.
Contoh Soal 2
Tentukan rasio antara suku pertama dan suku keenam dalam sebuah barisan aritmatika.
Untuk mencari rasio antara suku pertama dan suku keenam, kita perlu mengetahui suku pertama dan selisihnya. Jika kita mengetahui suku pertama (a) dan selisih (d), kita dapat gunakan rumus rasio:
Rasio = U6 / U1
Sebagai contoh, misalkan a adalah 2 dan d adalah 3.
Maka, suku keenam dalam barisan ini adalah:
U6 = a + (6-1) * d
U6 = 2 + 5 * 3
U6 = 2 + 15
U6 = 17
Jadi, rasio antara suku pertama dan suku keenam dalam barisan ini adalah 17 / 2 = 8.5.
Contoh Soal 3
Temukan suku ke-10 dan suku ke-12 dalam sebuah barisan aritmatika dengan selisih 4 dan suku pertama 2.
Untuk mencari suku ke-10 dan ke-12 dalam barisan ini, kita dapat menggunakan rumus Un = a + (n-1) * d.
Asumsikan suku pertama (a) adalah 2 dan selisihnya (d) adalah 4.
Untuk mencari suku ke-10:
U10 = 2 + (10-1) * 4
U10 = 2 + 9 * 4
U10 = 2 + 36
U10 = 38
Jadi, suku ke-10 dalam barisan ini adalah 38.
Untuk mencari suku ke-12:
U12 = 2 + (12-1) * 4
U12 = 2 + 11 * 4
U12 = 2 + 44
U12 = 46
Jadi, suku ke-12 dalam barisan ini adalah 46.
FAQ
1. Apa itu barisan aritmatika?
Barisan aritmatika adalah rangkaian bilangan dengan perbedaan yang tetap antara dua suku berturut-turutnya.
2. Apa rumus untuk mencari suku ke-n pada barisan aritmatika?
Rumus umum untuk mencari suku ke-n pada barisan aritmatika adalah Un = a + (n-1) * d, di mana Un adalah suku ke-n, a adalah suku pertama, n adalah posisi suku, dan d adalah selisih antara suku berturut-turut.
3. Apa yang dimaksud dengan selisih pada barisan aritmatika?
Selisih pada barisan aritmatika adalah perbedaan antara dua suku berturut-turut dalam barisan.
4. Apa yang terjadi jika selisih negatif dalam barisan aritmatika?
Jika selisih dalam barisan aritmatika negatif, maka kita dapat menganggap bahwa barisan tersebut berkurang.
5. Apakah selisih dalam barisan aritmatika hanya bisa angka bulat?
Tidak, selisih dalam barisan aritmatika bisa berupa bilangan riil.
6. Apakah ada hubungan antara barisan aritmatika dan deret aritmatika?
Ya, barisan aritmatika adalah rangkaian bilangan yang berurutan, sedangkan deret aritmatika adalah penjumlahan dari semua suku pada barisan aritmatika.
7. Apakah rumus untuk mencari suku ke-n berlaku untuk semua barisan aritmatika?
Ya, rumus Un = a + (n-1) * d berlaku untuk semua barisan aritmatika. Namun, perhatikan bahwa arti dari suku pertama (a), posisi suku (n), dan selisih (d) akan berbeda-beda tergantung pada barisan yang sedang kita bahas.
8. Apa cara membedakan barisan aritmatika dan barisan geometri?
Barisan aritmatika memiliki perbedaan tetap antara suku berturut-turutnya, sedangkan barisan geometri memiliki rasio tetap antara suku berturut-turutnya.
9. Berapa rumus untuk mencari suku ke-n dalam barisan geometri?
Rumus umum untuk mencari suku ke-n dalam barisan geometri adalah Un = a * r^(n-1), di mana Un adalah suku ke-n, a adalah suku pertama, r adalah rasio antara suku-suku berturut-turut, dan n adalah posisi suku yang ingin dicari.
10. Bagaimana mengidentifikasi apakah suatu deret bilangan adalah barisan aritmatika atau geometri?
Jika perbedaan antara suku berturut-turut konstan, maka deret tersebut adalah barisan aritmatika. Jika rasio antara suku berturut-turut konstan, maka deret tersebut adalah barisan geometri.
Kesimpulan
Pada artikel ini, kita telah membahas secara mendalam mengenai rumus suku ke-n pada barisan aritmatika. Dengan mengidentifikasi suku pertama dan selisih dalam barisan aritmatika, kita dapat menggunakan rumus Un = a + (n-1) * d untuk mencari suku ke-n dengan mudah. Contoh soal yang disertakan juga dapat membantu memperjelas konsepnya. Semoga artikel ini bermanfaat bagi pembaca dalam memahami cara mencari suku ke-n pada barisan aritmatika.







