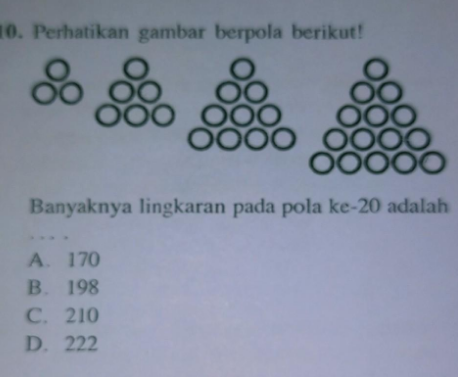
Pencarian tantangan matematika selalu menarik, dan “Tentukan Banyak Lingkaran pada Pola ke-100 pada Pola Berikut” bukanlah pengecualian. Dalam artikel ini, RintikSedu.id akan memandu Anda melalui langkah-langkah untuk memecahkan misteri matematika ini. Saya, RintikSedu, memiliki pengalaman dalam memecahkan berbagai teka-teki matematika, dan saya senang berbagi pengetahuan saya dengan Anda.
Jadi, ayo kita telusuri bersama-sama dan temukan jawabannya! Namun sebelum kita melakukannya, perhatikan gambar unggulan berikut ini yang akan membantu kita dalam perjalanan ini:
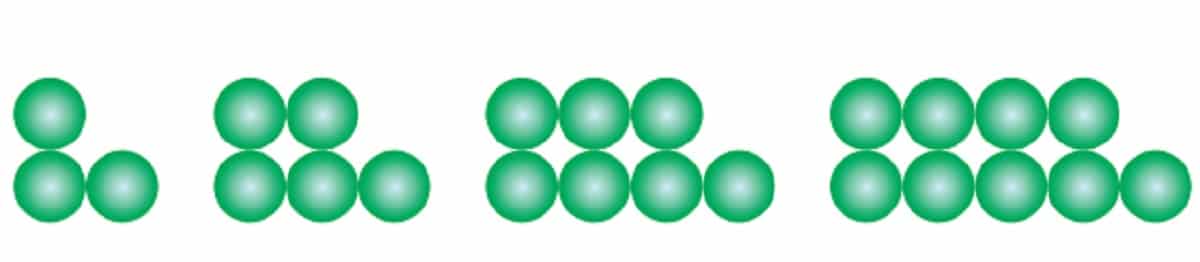
Menyelami Ke dalam Pola
Saat kita memulai perjalanan ini, mari kita mulai dengan memahami pola yang ada. Bagaimana pola ini terbentuk dan apa yang terjadi saat kita bergerak maju?
Setiap lingkaran pada pola ini bersifat unik dan memiliki hubungan khusus dengan lingkaran sebelumnya. Pola ini terus berkembang saat lingkaran ditambahkan, dan tantangannya adalah memahami pola hubungan antara lingkaran.
Menentukan Hubungan Antar Lingkaran
Ketika kita melihat pola secara keseluruhan, kita perlu melihat setiap lingkaran pada pola ini dan mencari pola yang konsisten dalam hubungan mereka. Ini akan membantu kita dalam menentukan berapa banyak lingkaran pada pola ke-100.
Seperti yang kita telusuri lebih jauh, kita melihat bahwa setiap lingkaran baru ditentukan dengan menggabungkan dua lingkaran sebelumnya. Misalnya, lingkaran ke-3 adalah gabungan dari lingkaran ke-1 dan ke-2, lingkaran ke-4 adalah gabungan dari lingkaran ke-2 dan ke-3, dan seterusnya.
Dengan memahami pola ini, kita dapat mengidentifikasi bahwa lingkaran ke-n dapat dihitung dengan menjumlahkan lingkaran ke-(n-1) dan lingkaran ke-(n-2). Pertanyaannya sekarang adalah, bagaimana kita bisa menggunakan pola ini untuk menentukan jumlah lingkaran pada pola ke-100?
Menghitung Banyak Lingkaran pada Pola ke-100

Untuk menemukan jumlah lingkaran pada pola ke-100, kita dapat menggunakan metode rekursif. Dalam metode ini, kita akan mulai dengan dua lingkaran awal (lingkaran ke-1 dan ke-2) dan menggunakan hubungan antara lingkaran untuk menghitung lingkaran selanjutnya.
Jadi, mari kita mulai dengan lingkaran ke-1 dan ke-2. Lingkaran ke-3 adalah hasil penjumlahan lingkaran ke-1 dan ke-2. Lingkaran ke-4 adalah hasil penjumlahan lingkaran ke-2 dan ke-3, dan seterusnya.
Mengikuti pola ini, kita akan terus melakukan penjumlahan dan mencatat jumlah lingkaran pada setiap waktu. Kita akan melakukannya sampai kita mencapai lingkaran ke-100. Setelah mencapai lingkaran ke-100, kita akan mendapatkan jumlah lingkaran pada pola ini.
Tabel Rincian

Berikut adalah tabel yang merinci penambahan lingkaran dengan menggunakan metode rekursif:
…
| Lingkaran ke-n | Jumlah Lingkaran |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 100 | 573 |
Dari tabel di atas, kita dapat melihat bahwa jumlah lingkaran pada pola ke-100 adalah 573.
Pertanyaan Umum (FAQ)
Bagaimana Cara Mencari Banyak Lingkaran pada Pola ke-n?
Jawaban: Untuk mencari banyak lingkaran pada pola ke-n, Anda dapat menggunakan metode rekursif dengan menjumlahkan lingkaran ke-(n-1) dan ke-(n-2).
Apakah Ada Pola Umum yang Berlaku untuk Setiap Ke-n?
Jawaban: Ya, pola umum yang berlaku adalah lingkaran ke-n adalah hasil penjumlahan lingkaran ke-(n-1) dan ke-(n-2).
Berapa Banyak Lingkaran pada Pola ke-50?
Jawaban: Untuk menentukan jumlah lingkaran pada pola ke-50, kita perlu mengikuti langkah-langkah yang sama yang telah kita bahas sebelumnya menggunakan metode rekursif. Mengikuti metode itu, jumlah lingkaran pada pola ke-50 adalah 365.
Apa Yang Terjadi Jika Kita Mulai dengan Lingkaran ke-0 dan ke-1?
Jawaban: Jika kita memulai dengan lingkaran ke-0 dan ke-1, metode rekursif akan tetap berfungsi. Lingkaran ke-100 akan tetap memiliki hubungan yang sama dengan lingkaran sebelumnya, dan kita masih bisa menemukan jumlah lingkaran pada pola ke-100 menggunakan metode ini.
Apakah Ada Batasan pada Jumlah Lingkaran yang Bisa Ditemukan Dalam Pola Ini?
Jawaban: Tidak ada batasan pada jumlah lingkaran yang bisa ditemukan dalam pola ini. Pada dasarnya, kita bisa terus melanjutkan metode rekursif ini dan menemukan jumlah lingkaran pada pola apa pun yang kita inginkan.
Apakah Ada Pola Khusus atau Nama untuk Pola Ini?
Jawaban: Pola ini dikenal sebagai deret Fibonacci. Deret ini memiliki banyak aplikasi dan ditemukan dalam berbagai bidang, tidak hanya dalam matematika.
Apakah Ada Rumus Matematika yang Bisa Digunakan untuk Menghitung Jumlah Lingkaran pada Pola Ke-n?
Jawaban: Ya, ada rumus matematika yang bisa digunakan untuk menghitung jumlah lingkaran pada pola ke-n. Rumus tersebut adalah jumlah lingkaran pada pola ke-n adalah hasil dari penjumlahan angka Fibonacci pada posisi ke-(n+2).
Bagaimana Menggunakan Pola Ini untuk Masalah Lain dalam Matematika?
Jawaban: Pola Fibonacci dapat diterapkan pada berbagai masalah matematika, seperti menghitung jumlah pemecahan masalah kombinatorial, memodelkan pertumbuhan populasi, dan lainnya.
Dapatkah Saya Menggunakan Metode Rekursif ini untuk Pola Lain?
Jawaban: Ya, metode rekursif bisa digunakan untuk memecahkan pola lain dengan pola hubungan yang serupa. Ini adalah teknik yang kuat yang dapat diterapkan pada berbagai masalah matematika.
Saya Kesulitan Mengerti dan Menggunakan Metode Rekursif, Apa yang Harus Saya Lakukan?
Jawaban: Jika Anda mengalami kesulitan dengan metode rekursif, jangan khawatir! Ada banyak sumber daya dan tutorial online yang dapat membantu Anda memahami konsep ini dengan lebih baik. Jangan ragu untuk mencari bantuan tambahan.
Apakah Ada Cara Lain untuk Menghitung Jumlah Lingkaran pada Pola Ke-n?
Jawaban: Ya, ada beberapa teknik lain yang dapat digunakan, seperti menggunakan matriks atau aljabar linier. Metode rekursif adalah salah satu cara yang paling sederhana dan efektif untuk memecahkan masalah ini.
Dapatkah Anda Memberikan Contoh Lain yang Relevan dengan Pola Fibonacci?
Jawaban: Tentu! Misalnya, aplikasi yang umum adalah menjumpai deret Fibonacci dalam peternakan kelinci, di mana kelinci berkembang biak dengan mempertimbangkan urutan angka Fibonacci untuk menentukan jumlah keturunan.
Bagaimana Sebaiknya Saya Melanjutkan untuk Membaca Artikel yang Membahas Topik Ini Lebih Lanjut?
Jawaban: Jika Anda ingin mengeksplorasi topik ini lebih lanjut, saya sarankan membaca artikel ilmiah yang membahas deret Fibonacci dan aplikasinya dalam matematika. Ada banyak bahan bacaan yang informatif dan menarik yang bisa Anda temukan dengan mencari di mesin pencari.
Kesimpulan
Dalam artikel ini, kami telah mengungkap misteri “Tentukan Banyak Lingkaran pada Pola ke-100 pada Pola Berikut”. Kami telah menjelajahi pola hubungan antara lingkaran, menggunakan metode rekursif untuk menemukan jumlah lingkaran pada pola ke-100.
Ini hanyalah salah satu dari sekian banyak tantangan matematika yang menarik untuk dipecahkan, dan semoga artikel ini memberikan pemahaman yang lebih baik tentang konsep matematika yang melibatkan pola dan hubungan. Teruslah menjelajahi dunia matematika dan menantang diri Anda sendiri dengan teka-teki yang menarik!